Okay, so as I point out in that italicized chunk at the bottom of every one of my posts, my profession is teaching physics. That involves working up a lot of lecture notes (even if you're teaching in a more interactive format, some of it is going to be lecture unless you have a lot of co-teachers helping run the classroom), and revising them when (not if) you find they're not working the way you'd like.
In wrapping up the latest revision of my Physics 1 notes, I worked out a hopefully improved way to explain entropy, that bugaboo of many superhero and sci-fi stories. No, I'm not going to dump my lecture notes here, they're meant for an audience that has already gone over a number of other concepts, and contain math that's not really needed for this article. But I figured that the core explanation, with some elaboration, would be useful in helping people understand just what entropy is.
A neat room has lower entropy than a messy room, but what does it mean to be neat versus messy? Mainly it comes down to possibilities, but to really get down to brass tacks I'm going to have to introduce a few more technical terms.
Macrostates and Microstates
Nope, not talking about Texas versus Rhode Island. As a very rough definition, a macrostate is something you can make sense of on the scale of a person, without going into unpleasant amounts of detail. By contrast, a microstate is all about the unpleasant detail. These details are often microscopic, but they don't have to be.
For instance, most averages can be thought of as macrostates, while the lists of all the numbers that went into the average are microstates. If the number of things is fairly small, then we can meaningfully deal with both the average and all the raw data...you can remember the ages of everyone in your family fairly easily, but if you want the ages of everyone in your city an average might be more useful.
For instance, the median age of residents of Miami FL is 39.1 years old, while the median age of U.S. citizens overall is 37.8 years old. (Median is a kind of average that looks at a midpoint: as many people in Miami are older than 39.1 as are younger than 39.1.) Without having to know everyone's ages, I can say that residents of Miami are a bit older than Americans as a whole. 37.8 years old is the macrostate of "how old are Americans," whereas the microstate is the list of the ages of everyone in the country.
How many microstates per macrostate?
We're getting closer to entropy, trust me.
Rather than play with millions of people, let's drop down to a couple of regular cube-shaped dice, or d6's in gamer parlance. If you roll two dice (2d6) and add the results together, you get a number from 2 to 12. Assume they're different colors, so you can easily tell "4 and 3" apart from "3 and 4".
There's five ways to get a result of 8 when rolling two dice: 2+6, 3+5, 4+4, 5+3, and 6+2. This macrostate therefore has five microstates. If all you know is that the total is 8, you don't know which of the five microstates got you there, just like knowing that the median age of Americans is 37.4 doesn't tell you my age.
Now consider "8 the hard way," with the hard way being when you have the same number on each die. That's just one microstate, 4+4. 8 the hard way is less likely than 8 not the hard way, one microstate versus four. If all you know is that the total is 8, and you were asked if it was 4+4, you'd be right to say, "probably not."
The more microstates in a particular subset, the more likely it is that one of those microstates will be what you get when you see the associated macrostate.
You're certainly allowed to get 8 the hard way, but it's four times more likely that a roll of 8 won't be doubles.
So, to go back to median age, you could get 37.8 by having 150-some million teenagers, one person who is 37.8 years old, and as many octogenarians as you have teenagers. That's a valid way to get the macrostate. But it's a lot less likely than having a bunch of people in every age group.
Dvandom, aka Dave Van Domelen, is an Assistant Professor of Physical Science at Amarillo College, maintainer of one of the two longest-running Transformers fansites in existence (neither he nor Ben Yee is entirely sure who was first), long time online reviewer of comics, thinks "decreasing the entropy of my collection" sounds classier than "stuffing toy robots into boxes", is an occasional science advisor in fiction, and part of the development team for the upcoming City of Titans MMO.
 |
| Marvel's Entropy. And here I thought that was (insert creator name here). |
A neat room has lower entropy than a messy room, but what does it mean to be neat versus messy? Mainly it comes down to possibilities, but to really get down to brass tacks I'm going to have to introduce a few more technical terms.
Macrostates and Microstates
 |
| More of a ministate. |
Nope, not talking about Texas versus Rhode Island. As a very rough definition, a macrostate is something you can make sense of on the scale of a person, without going into unpleasant amounts of detail. By contrast, a microstate is all about the unpleasant detail. These details are often microscopic, but they don't have to be.
For instance, most averages can be thought of as macrostates, while the lists of all the numbers that went into the average are microstates. If the number of things is fairly small, then we can meaningfully deal with both the average and all the raw data...you can remember the ages of everyone in your family fairly easily, but if you want the ages of everyone in your city an average might be more useful.
For instance, the median age of residents of Miami FL is 39.1 years old, while the median age of U.S. citizens overall is 37.8 years old. (Median is a kind of average that looks at a midpoint: as many people in Miami are older than 39.1 as are younger than 39.1.) Without having to know everyone's ages, I can say that residents of Miami are a bit older than Americans as a whole. 37.8 years old is the macrostate of "how old are Americans," whereas the microstate is the list of the ages of everyone in the country.
How many microstates per macrostate?
We're getting closer to entropy, trust me.
Rather than play with millions of people, let's drop down to a couple of regular cube-shaped dice, or d6's in gamer parlance. If you roll two dice (2d6) and add the results together, you get a number from 2 to 12. Assume they're different colors, so you can easily tell "4 and 3" apart from "3 and 4".
 |
| 8 the hard (and sharp-edged) way. |
Now consider "8 the hard way," with the hard way being when you have the same number on each die. That's just one microstate, 4+4. 8 the hard way is less likely than 8 not the hard way, one microstate versus four. If all you know is that the total is 8, and you were asked if it was 4+4, you'd be right to say, "probably not."
The more microstates in a particular subset, the more likely it is that one of those microstates will be what you get when you see the associated macrostate.
You're certainly allowed to get 8 the hard way, but it's four times more likely that a roll of 8 won't be doubles.
So, to go back to median age, you could get 37.8 by having 150-some million teenagers, one person who is 37.8 years old, and as many octogenarians as you have teenagers. That's a valid way to get the macrostate. But it's a lot less likely than having a bunch of people in every age group.
Roughly speaking, entropy is a measure of how many ways there are to get a particular type of microstate within a given macrostate.
8 the hard way has less entropy than 8 not-the-hard way, as there are fewer ways to get that type of microstate. If your macrostate is "all of my clothing is in my room," the subset where "all of my clothing is neatly put away" has way fewer microstates than all the ways the clothing could be scattered about the room. A messy room has higher entropy because there's so many more ways a room can be messy than there are ways a room can be neat.
Now For Thermodynamics
Generally, when we try to do actual calculations of entropy, the macrostate in question is temperature. When you measure absolute temperature (usually in the Kelvin scale), the temperature is related to the average energy of each molecule. In other words, multiplying the temperature by a particular constant will give you the average motion (kinetic) energy of a molecule.
Absolute zero is like rolling a 2 on 2d6, then. The motion energy of a molecule can't be negative (it's moving or it isn't, it can't anti-move), so if the average is zero, then every molecule has to be at zero energy too. Entropy is at a minimum at absolute zero, because there's only one microstate per macrostate, period. Higher temperatures mean more average motion, and more microstates, and more possibility for entropy. In fact, since most things that raise temperature tend to raise the number of microstates in the most likely patterns, we tend to say that higher temperatures mean more entropy. (There's an idealized process that can raise temperature without increasing entropy, but you never actually get ideal conditions, so we might as well stick with hotter = more entropy.)
At higher temperatures, it's certainly possible that one molecule has all the energy and the rest are unmoving. The total number of microstates for that equals the total number of molecules, each one having a chance of hogging all the energy. That seems like it'd be a big number, and it certainly is, often on the scale of N = 1,000,000,000,000,000,000,000,000 or so. But the total number of microstates is often a number so much bigger that we don't even try to write it down as a number, we just hide behind things like e raised to the N power. "One molecule has all the energy" is pretty unlikely when you only have two molecules in your set, now consider when you have a few septillion molecules. Yeah, good luck with that.
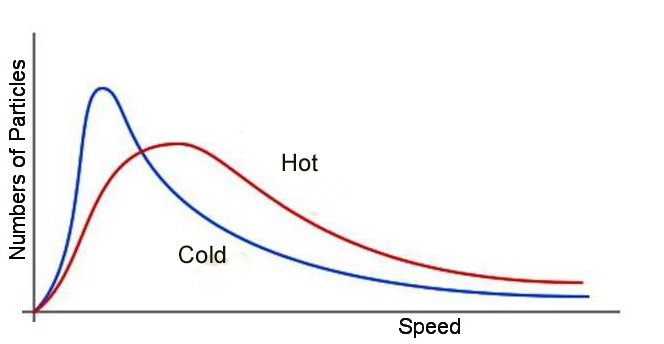
Basically, the most likely microstates will have a most likely energy, with a lot of molecules near that value, and fewer in each "bin" as you get farther away in either direction. The Maxwell-Boltzmann Distribution is an example of one such spread of microstates, for molecule speed rather than motion energy (the two are related, though). There are far more microstates for gas molecules that fall into this pattern than pretty much any other pattern, so this pattern has the highest entropy and is the most likely. If you take two gases at different temperatures and put them in a small tank, eventually they'll settle down to a single temperature following the Maxwell-Boltzmann Distribution, rather than staying as a hot gas next to a cold gas. The entropy of a single MBD is greater than that of two overlapping different ones, and if you don't do anything about it, entropy always increases. That's the Second Law of Thermodynamics.
HOWEVER!
"If you don't do anything about it" is a big if. I can cheat and rig dice to be more likely to roll doubles. If I pre-select the people whose ages I'm averaging, I can get a room full of teenagers and octogenarians if I really want to annoy them all.
As long as you can bring in energy from outside, you can always force unlikely microstates. You can clean up your room, you can separate gases, you can keep the hot side hot and the cool side cool. But it takes the input of energy from outside the system.
Earth is full of all sorts of lovely low-entropy patterns, but we're constantly receiving energy from the Sun. Plants use that energy to turn high-entropy air and water and dirt into lower-entropy plants. Herbivores use energy stored in plants to turn more air and water and the plant matter into lower entropy herbivores. And so forth. Cut off the sun, and plants revert to higher entropy (dead) states. If an animal stops eating, it eventually reverts to a higher entropy state. And so it goes. You can decrease entropy as long as you can bring in energy from outside to pay for it.
It turns out that however much you decrease the entropy inside, you increase the entropy outside by more, usually giving at least some of it to whatever provided the energy. The Second Law of Thermodynamics says that once you account for all the places energy can come from or go to, the overall entropy has to increase. The key is to increase it in places that don't matter as much to you, like outer space or at least inside the bedroom closet.
Entropy and the Multiverse
In speculative fiction, things get a little trickier. What if you can dump your entropy into another reality entirely? You need to broaden your definition of "all the places energy can come from," and some settings (like comics) are remarkably willing to come along and say there's a bigger everything this year than there was last year (Multiverse...no, OMNIverse! No, even bigger than that!). The result is that entropy may not be as big of a problem as in real life...not that it's a huge problem as long as the Sun keeps shining. (See Asimov's The Last Question for dealing with the issue in a SF universe without an outside to steal from.)
Eventually, though, you can figure that there will come an End of Time, when entropy catches up to the universe and reaches its maximum. One definition of the forward direction of time is that it's the direction in which entropy increases...but once entropy is as high as it can get, how can you tell time is moving forwards or backwards? In that case, time literally ends, because there's no longer a distinction between directions.
As long as nothing else weird happens (like a Big Rip), the end state of the universe is a sort of Maxwell-Boltzmann Distribution of photons, a uniformly cool universe with no particular patterns, because all of the unlikely patterns have been eliminated by increasing entropy. (One of the troubling things about the "Big Crunch" model of the end of the world is that at some point time goes forwards and overall entropy decreases, until everything is in the same place and there's exactly one microstate...even if there's a bounce before zero, it's still got decreasing entropy. We're pretty sure now that there won't be a Big Crunch, sorry Galactus.)
This is, of course, a boring place to set a grand citadel, because grand citadels can't exist. They're way too unlikely of microstates to survive to the End of Time. No Time Trappers either. As soon as something arrives at the End of Time, it ceases to be the End of Time, and time starts ticking again for however long it takes for the newcomer to die and decompose into photons. Which, granted, is a pretty long time. But "Citadel At Almost The End Of Time" doesn't really have the same ring to it, eh?
Is Maximum Entropy also Maximum Order?
Nope. Maximum order would be a specific microstate, everything in its place. The Maxwell-Boltzmann Distribution looks like a specific pattern, true. But it's just saying "some molecules doing this, some molecules are doing that" without saying anything about which molecule is doing what. You know the dice add to 7, but you don't know what the first die says, it could be any number. Maximum order would be a specific pattern always being followed, like always a specific combination such as 1 and 6, or each die always advancing by 1 on each roll until it hits 6, then rolling 1 the next time.
The visual uniformity of the entropic end state of the universe is only an illusion of order. Order, to the extent humans understand it, requires low entropy patterns. Maximum order would be all the photons having the same energy as the average energy, like having a country where everyone is exactly 37.8 years old. And leaving aside a weird bit of pre-Crisis retcon, that would make everyone too old to be in the Legion of Super-Heroes....
As long as you can bring in energy from outside, you can always force unlikely microstates. You can clean up your room, you can separate gases, you can keep the hot side hot and the cool side cool. But it takes the input of energy from outside the system.
 |
| Sweet, sweet, entropy sink. |
Earth is full of all sorts of lovely low-entropy patterns, but we're constantly receiving energy from the Sun. Plants use that energy to turn high-entropy air and water and dirt into lower-entropy plants. Herbivores use energy stored in plants to turn more air and water and the plant matter into lower entropy herbivores. And so forth. Cut off the sun, and plants revert to higher entropy (dead) states. If an animal stops eating, it eventually reverts to a higher entropy state. And so it goes. You can decrease entropy as long as you can bring in energy from outside to pay for it.
It turns out that however much you decrease the entropy inside, you increase the entropy outside by more, usually giving at least some of it to whatever provided the energy. The Second Law of Thermodynamics says that once you account for all the places energy can come from or go to, the overall entropy has to increase. The key is to increase it in places that don't matter as much to you, like outer space or at least inside the bedroom closet.
Entropy and the Multiverse
In speculative fiction, things get a little trickier. What if you can dump your entropy into another reality entirely? You need to broaden your definition of "all the places energy can come from," and some settings (like comics) are remarkably willing to come along and say there's a bigger everything this year than there was last year (Multiverse...no, OMNIverse! No, even bigger than that!). The result is that entropy may not be as big of a problem as in real life...not that it's a huge problem as long as the Sun keeps shining. (See Asimov's The Last Question for dealing with the issue in a SF universe without an outside to steal from.)
 |
| Not Rokk. Nope. |
As long as nothing else weird happens (like a Big Rip), the end state of the universe is a sort of Maxwell-Boltzmann Distribution of photons, a uniformly cool universe with no particular patterns, because all of the unlikely patterns have been eliminated by increasing entropy. (One of the troubling things about the "Big Crunch" model of the end of the world is that at some point time goes forwards and overall entropy decreases, until everything is in the same place and there's exactly one microstate...even if there's a bounce before zero, it's still got decreasing entropy. We're pretty sure now that there won't be a Big Crunch, sorry Galactus.)
This is, of course, a boring place to set a grand citadel, because grand citadels can't exist. They're way too unlikely of microstates to survive to the End of Time. No Time Trappers either. As soon as something arrives at the End of Time, it ceases to be the End of Time, and time starts ticking again for however long it takes for the newcomer to die and decompose into photons. Which, granted, is a pretty long time. But "Citadel At Almost The End Of Time" doesn't really have the same ring to it, eh?
Is Maximum Entropy also Maximum Order?
Nope. Maximum order would be a specific microstate, everything in its place. The Maxwell-Boltzmann Distribution looks like a specific pattern, true. But it's just saying "some molecules doing this, some molecules are doing that" without saying anything about which molecule is doing what. You know the dice add to 7, but you don't know what the first die says, it could be any number. Maximum order would be a specific pattern always being followed, like always a specific combination such as 1 and 6, or each die always advancing by 1 on each roll until it hits 6, then rolling 1 the next time.
The visual uniformity of the entropic end state of the universe is only an illusion of order. Order, to the extent humans understand it, requires low entropy patterns. Maximum order would be all the photons having the same energy as the average energy, like having a country where everyone is exactly 37.8 years old. And leaving aside a weird bit of pre-Crisis retcon, that would make everyone too old to be in the Legion of Super-Heroes....
Dvandom, aka Dave Van Domelen, is an Assistant Professor of Physical Science at Amarillo College, maintainer of one of the two longest-running Transformers fansites in existence (neither he nor Ben Yee is entirely sure who was first), long time online reviewer of comics, thinks "decreasing the entropy of my collection" sounds classier than "stuffing toy robots into boxes", is an occasional science advisor in fiction, and part of the development team for the upcoming City of Titans MMO.
Entropy for Beginners (or Enders?)
![Entropy for Beginners (or Enders?)]() Reviewed by Dvandom
on
Wednesday, March 21, 2018
Rating:
Reviewed by Dvandom
on
Wednesday, March 21, 2018
Rating: